Label Smoothing & Calibration 논문 리뷰

in projects on Blog, Github, Pages, Jekyll, Spacy


서론

Rethinking the Inception Architecture for Computer Vision에서 처음 제시되고 현재 여러 SOTA 모델들의 훈련에 활용된 Label Smoothing 기법에 대해 정리한다. Label Smoothing 기법이 모델 학습에 미치는 영향들이 제시된 When Does Label Smoothing Help?를 바탕으로 포스트가 작성되었다. https://arxiv.org/pdf/1906.02629.pdf

과적합되는 현상은 모델 성능을 떨어뜨리는 주요 원인으로 과적합된 모델은 학습용 데이터 에 대해 높은 성능을 보이는 반면, 학습에 사용되지 않은 검증용 데이터 에 대해서는 제대로된 추론을 하지 못한다. 대표적으로 Dropout과 Label Smoothing이 과적합을 방지하기 위해 모델에 사용되며, 높은 성능 향상 결과를 보인다. 본문에서는 일반화 기법들 중 여러 SOTA 모델에 적용된 기법인 Label Smoothing에 대해 다룬다.

Label Smoothing은 […0 1 0…]의 하드 타깃 레이블 대신 […0.01 0.92 0.01…]의 평활화된 소프트 타겟 레이블을 모델 학습에 사용해 성능을 개선한다. 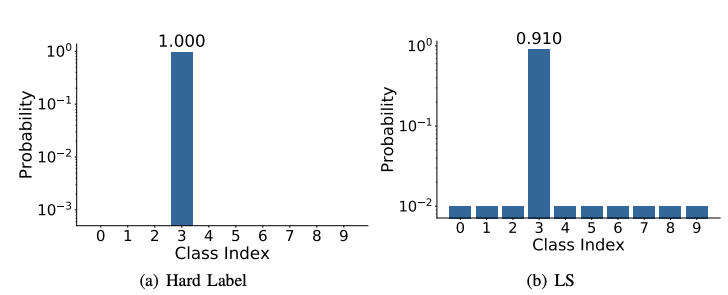이미지

Label Smoothing은 모델 일반화를 포함해 다음과 같은 특징들을 갖는다.

  • 모델 일반화 및 학습속도 개선 ( improve generalization & learning speed )
  • 모델 보정 효과 개선 ( improve model calibration )
  • 지식 증유에 보이는 역효과 ( less effective to knowledge distillation )

위 특징들은 아래에서 자세히 설명할 예정이다.

Label Smoothing 기법 소개

기법을 이해하기 위해 그 핵심이 되는 Cross-Entropy Loss에 대한 사전지식이 필요하다.

Cross Entorpy Details --- Entropy는 정보이론에서 정보를 나타내는 단위로 정보의 불확실성이라고도 한다. 정보에 대한 확률분포를 기반으로 계산되며 정보량에 대한 식은 다음 같다. $$ H(p) = -\sum_i p_i log p_i \\ $$ 정보이론에서 Relative Entropy 혹은 Kullback-Leibler distance를 사용해 두 가지 정보(Entropy)를 비교한다. 두 정보가 비슷하면 비슷할수록 0에 가까운 값을 갖고, 다르면 다를 수록 큰 값을 갖는다. `Kullback-Leibler distance로 두 확률분포 사이의 유사도에 대한 측정이 가능하다.` $$ D_{KL}(p||q) = - p_i \cdot log \frac{p_i}{q_i} $$ `Cross Entorpy`는 Kullback-Lebler distance와 동일한 식으로 모델 출력과 hard 레이블의 유사도를 계산하는 식이다. 다음은 categorical cross entropy의 식이다. $$ CE = -\sum p_i log q_i $$ 모델의 출력 $q_i$와 hard label $p_i$ 사이의 relative entropy를 계산한 식으로 하드 레이블은 $p_i$가 0 또는 1의 값만 갖기 때문은 Kullback-Leibler distance는 위와 같이 Cross Entorpy 식으로 간략히 표현된다. 즉, Cross-Entropy loss를 사용한 모델은 모델 출력과 하드 라벨의 분포가 같아지도록 학습된다. Kullback-Leibler distance는 줄여서 `KL Divergence`라고도 한다. --- </div>

다중 클래스 분류(multi-class classification) 모델은 신경망 마지막에 위치하는 소프트맥스 함수의 출력 과 하드 라벨 사이의 유사도를 높이는 방식으로 학습되며, 크로스 엔트로피 손실을 최소화하며 목적을 달성한다.

# Cross-Entropy Loss
criterion = nn.KLDivLoss(reduction="none")
ce_loss = criterion(torch.log_softmax(x, dim=1), hard_dist)

라벨 스무딩은 모델의 출력을 하드 라벨과 비교하는 대신 소프트 라벨과 비교하며 소프트 라벨은 균등 분포 함수(uniform distribution)와 하드 라벨의 weighted mixture를 사용한다. 반면, 라벨 스무딩이 적용된 모델은 소프트맥스 함수의 출력 과 소프트 라벨 사이의 유사도를 높이는 방식으로 학습된다. 소프트 라벨은 균등 분포 함수(uniform distribution)와 하드 라벨의 weighted mixture로 구해진다. \[y_k^{LS} = y_k (1-\alpha) + \alpha/K\]

# Label Smoothing Loss
criterion = nn.KLDivLoss(reduction="none")
soft_dist = hard_dist * (1-alpha) + norm_dist / K
lsm_loss = criterion(torch.log_softmax(x, dim=1), soft_dist)

라벨 스무딩은 아래에 코드에서 구체적으로 구현되어있다.

Penultimate Layer Representations 시각화

라벨 스무딩이 적용된 모델 은 올바른 클래스와 잘못된 클래스들 사이의 값들이 균등한 거리로 분포되도록 학습된다. 예로 1번이 올바른 클래스이라면, (1,2) (1,3), (1,4) … 의 클래스들이 비슷한 거리를 두고 분포한다. 거리 정보는 모두 $ \alpha $와 관련된 값을 갖는다.

반면, 하드 라벨로 학습된 모델 은 올바른 클래스가 다른 클래스들에 비해 굉장히 큰 예측 값으로 예측되고, 잘못된 클래스들 사이의 예측 값 또한 거리가 불균등하도록 학습된다.

라벨 스무딩을 시각화하면, 정답 클래스를 중심으로 다른 클래스들이 아치 모양으로 분포된 형태를 보인다.

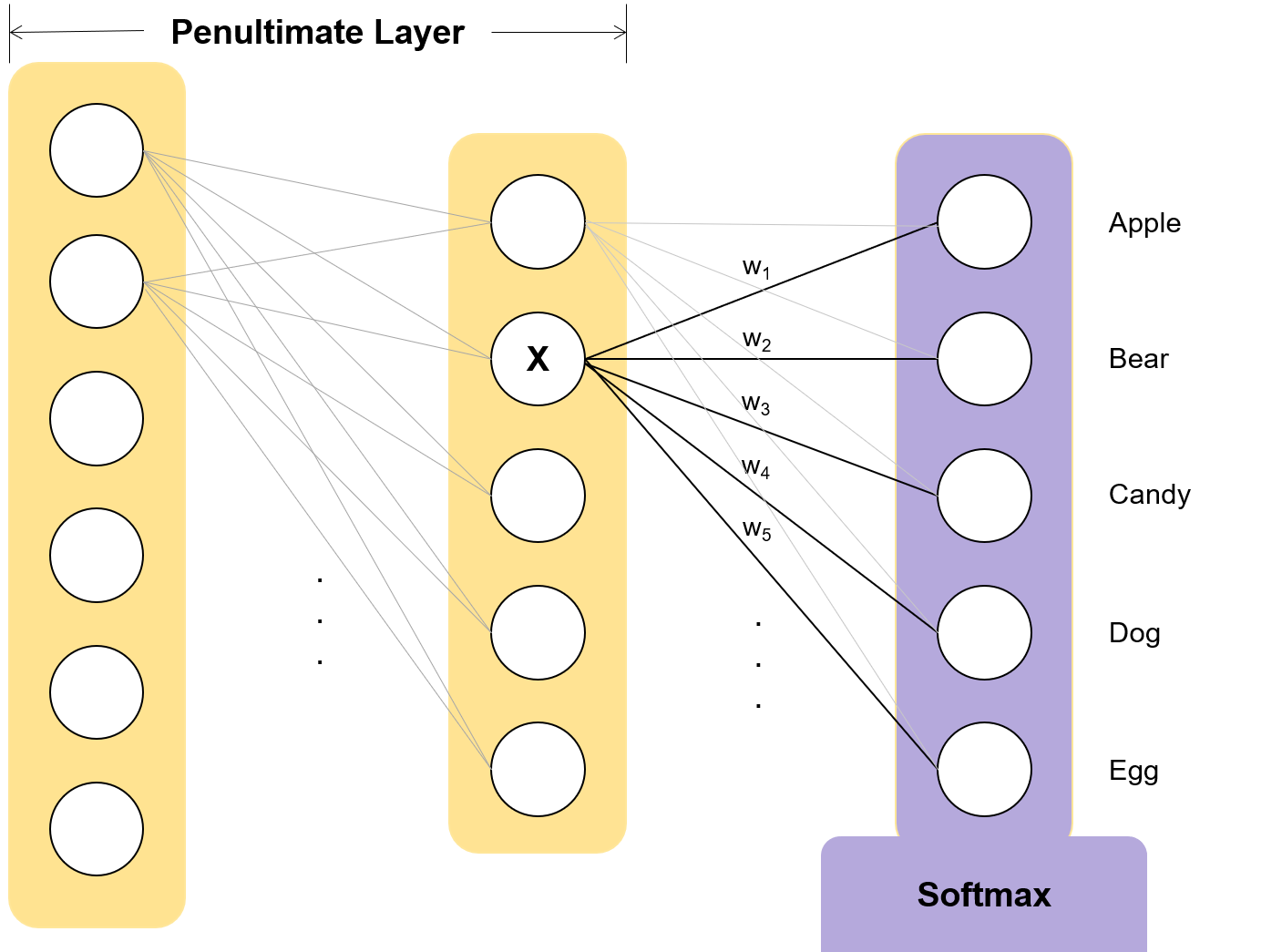
Penultimate Layer의 출력 값을 사용해 직관적으로 설명할 수 있다. Fully-connected, 소프트맥스 계층 바로 직전 계층을 Penultimate 계층이며

이미지

그림에서 2번째 “hidden”이 penultimate 계층의 activation 즉, 출력 값이다.

Penultimate 계층의 출력 값 중 하나인 X 로 예측 값을 구하려고 하며 Apple, 1번 클래스가 이미지 인식의 답이라고 가정해보자. 클래스 k에 대한 소프트맥스의 출력은 다음과 같다. \[Pr(k) = \frac{e^{x^Tw_k}}{\sum e^{x^Tw_i}}\]

다음 확률은 계층 출력 x 와 각 클래스 출력과 관련된 $w_k$ 사이의 유클리드 거리와 관련 지을 수 있다.

\(||x-w_k||^2 = x^T x - 2x^T w_k + w_k^T w_k\) $x^Tx$ 는 모든 클래스에서 같은 값을 갖고 $w^Tw$는 대부분 클래스에서 상수의 값을 갖기 때문에 소프트맥스 함수를 통해 모델 출력에서 배제할 수 있다. \[\frac{e^{-||x-w_k||^2}}{\sum e^{-||x-w_i||^2}} = \frac{e^{ -x^T x + 2x^T w_k - w_k^T w_k}}{\sum e^{ - x^T x + 2x^T w_i - w_k^T w_i}} = \frac{e^{2x^Tw_k}}{\sum e^{2x^Tw_i}} = Pr(k)\]

올바른 클래스의 $w_k$와 같아지도록, 잘못된 클래스의 $w_k$와 멀어지도록 학습된다고 볼 수 있다. 라벨 스무딩은 잘못된 클래스의 $w_k$와 멀어지는 것 뿐만 아니라 각각의 거리를 동일하게 만들어준다 그 거리는 $\alpha$와 관련된 값이다.

penultimate 계층 출력이 $w_1$과 가깝우면서 $w_2, w_3, …$ 와 같은 거리를 갖도록 모델이 훈련된다. $w_1$ 과의 거리를 최소화 하는 기존 방식에 제약조건(Constraint)를 추가해 학습하는 것으로 볼 수 있다. $w_k$ 는 클래스 k와 밀접한 관계를 갖는 값으로 각각의 클래스를 대표하는 값이다.

이러한 라벨 스무딩의 특징을 관찰하기 위해 다음과 같은 시각화 방법을 제시한다.

  1. 데이터셋에서 3개 클래스를 선택
  2. 세 클래스의 가중치 템플릿이 교차하는 평면, 직교 기교 탐색
  3. 세 클래스로부터 추출된 Penultimate 계층 값들을 직교 기저 평면에 투영

라벨 스무딩이 적용된 모델들의 일반적인 특징인지 확인하기 위해 여러 데이터셋을 사용해 검증한다.

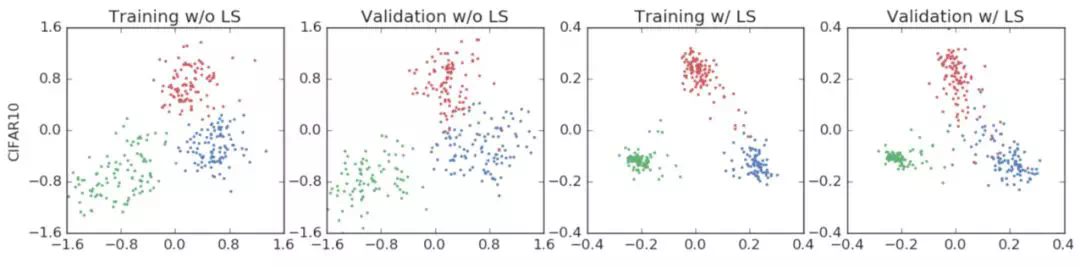이미지 클래스 : 비행기, 오토바이, 새 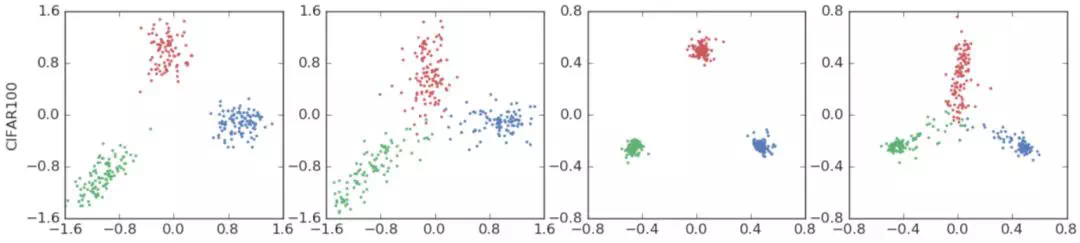이미지 클래스 : 비버, 돌고래, 수달 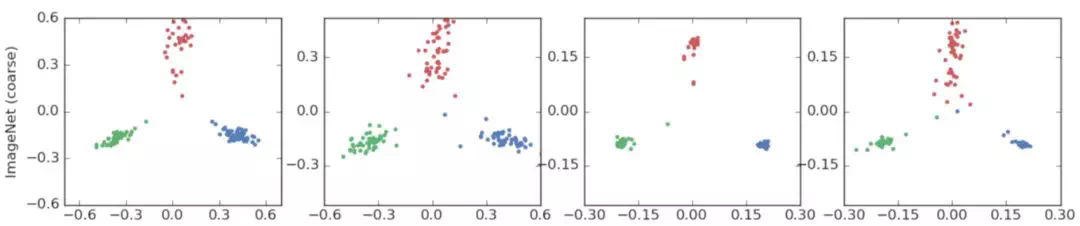이미지 클래스 : 텐치(tench), 미어캣(meerkat), 칼(cleaver) 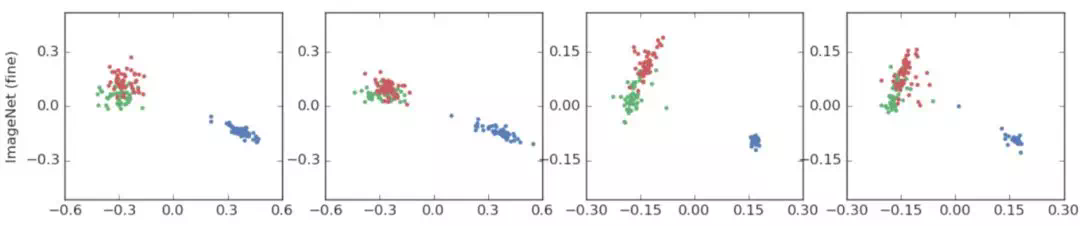이미지 클래스 : 장난감 푸들, 모형 푸들, 텐치(파랑) 의미론적으로 비슷한 클래스 2개와 전혀 다른 클래스 하나를 비교한다. 텐치 클래스를 두고 다른 두 클래스가 아치 형태로 분포하는 것을 확인할 수 있다. 또한, 푸들 클러스터와 텐치 클러스터 사이에 연속적으로 변화하는 정보가 라벨 스무딩을 하면 사라진다 이러한 정보가 사라지기 때문에 지식 증류에 악영향을 미친다.

이미지

포스트에서 더 자세한 내용을 확인할 수 있다.

Model Calibration 효과

모델 보정(calibration)에 대한 자세한 설명은 details에 자세히 설명되어 있다.

Model Calibration Details --- 모델은 예측하기 전에 sigmoid 또는 softmax 계층을 통해 0과 1 사이의 분포로 바뀐다 우리는 주로 이 값을 클래스로 분류할 확률로 해석하지만 On Calibration of Modern Neural Networks 을 확인하면 요즘 모델들은 정확도는 높지만 모델 보정이 되어 있지 않다고 주장한다. 모델이 보정됬다고 하면 모델이 소프트맥스 출력으로 0.9 인 경우들을 모아 실제로 이 클래스로 분류되는지 확인한다면 90% 이 클래스로 분류되어야한다 그러나 실제로 모델들을 보면 그렇지 않다 그림은 imagenet 모델이 보정이 되어 있는지 보여주는 그래프이다 bin은 20으로 사용해 표현된다. 0.05 간격으로 그래프를 만든다 [0.9,0.95] 사이로 예측되는 값들을 모아서 실제로 그렇게 예측되는지 확인한다. 에측될 확률과 클래스 정확도의 차이를 빨갛게 표현한다 빨간색이 진할수록 분포하는 값이 많다는 의미이다 모델 보정이 잘되어 있는지 확인하는 지표로 Expected Calibration Error(ECE)를 사용하며 식은 다음과 같다. $$ ECE = \sum_{b=1}^{B} \frac{n_b}{N} |acc(b) - conf(b)| $$ 무조건 정확도만 높으면 그만 아닌지 생각할 수 있다. 그러나 greedy-search 또는 beam-search가 사용되는 분야에는 영향이 클수도 있다. beam seach는 단어가 예측될 확률로 소프트맥스의 출력값을 사용하기 때문이다. 사과를 예측하고 싶다. beamsearch를 통해서 수를 사로 교정해줄 것을 기대하고 싶다. 그러나 수에대한 예측 확률이 너무 높아 이러한 교정이 되지 않는다 모델 보정이 제대로 이루어진다면 사과를 예측할 확률이 더 높아질 것이다. [포스트](https://github.com/hollance/reliability-diagrams)에서 더 자세한 내용을 확인할 수 있다. --- </div>

요약하면, 모델 보정(calibration)이 잘된 모델은 소프트맥스 출력값 과 실제 예측 확률 이 거의 같은 값을 갖는다.

모델이 얼마나 보정되어있지 측정하는 수치 expected calibration error(ECE)를 사용하며, Temperature과 라벨 스무딩의 두 기법을 비교한다.

소프트맥스 출력값이 한 쪽으로 너무 치우치지 않도록 조정한다. \[Pr(k) = \frac{e^{\frac{x_k}{T}}}{\sum e^{\frac{x_i}{T}}}\]

소프트맥스 출력 값의 수치는 다음과 같이 변한다.

https://3months.tistory.com/491T=0https://3months.tistory.com/491T=2https://3months.tistory.com/491T=10

출처: https://3months.tistory.com/491

T를 크게 줄 수록 각 확률 값들의 차이가 줄어듬을 확인 할 수 있다. T=2 일 때와 T=10 일때의 값이다. T 값은 특정 클래스의 확률값이 너무 커지지 않도록 해 모델 보정에 도움을 준다.

실험은 15-bin reliability diagram 이미지

이미지

Temperature을 사용한 것 만큼의 모델 보정 효과를 낼 수 있음을 확인 할 수 있다.

Beam Search에서의 영향을 확인하는 그림이다. 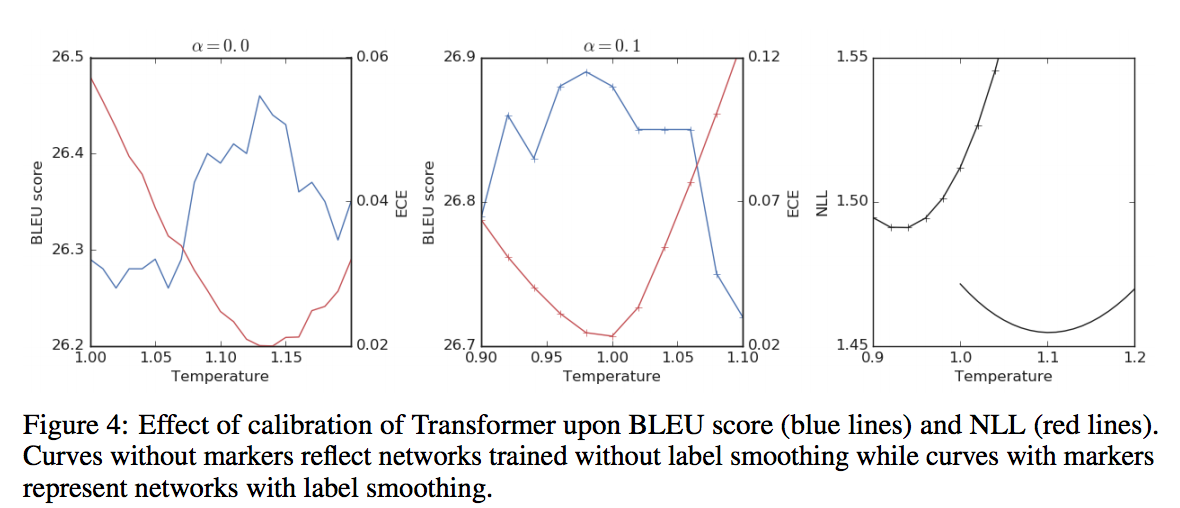이미지

라벨 스무딩은 ECE를 비슷하게 가져 가면서 BLEU 점수(blue)에서 T에 비해 더 좋은 성능을 낸다.

Knowledge Distillation에서의 악영향

이미지

클래스 : 장난감 푸들, 모형 푸들, 텐치(파랑)

또한, 푸들 클러스터와 텐치 클러스터 사이에 연속적으로 변화하는 정보가 라벨 스무딩을 하면 사라진다.

푸들이 얼마만큼의 텐치인지 정보가 사라진다.

정보를 잃는 것은 지식 증유에서 좋은 영향을 주지 못한다.

오히려 학생 모델을 혼자서 학습한 것이 더 잘나올 때도 있었다.

이를 증명하기 위해 정보이론의 상호의존정보(mutual information)을 사용한다. \[I(X;Y) = H(Y) - H(Y|X) = E_{X,Y}[-log(\sum{_x}p(y|x)p(x) + log(p(y|x))]\]

정보이론을 배우면 당연한 말이지만 $ H(X|Y) $ 를 구할 수 없어서 $ H(Y) = -log(\sum{_x}p(y|x)p(x) $의 복잡한 식이 사용된다. 몬테카를로 샘플링을 사용해 구해진 닫힌 형태(closed-form)의 식은 논문에서 확인 가능하다.

X : N 샘플에 대해서 discrete variable representation 에 대해 K 클래스의 차이 Y : N 샘플에 대해서 continuos representation 에 대해 K 클래스의 차이

2개 subset 600 샘플에 대해 측정한 mutual information이다.

라벨 스무딩을 사용하면 차이에 대한 정보를 더 많이 잃는다.

Label Smoothing 구현

import torch
from torch import nn
torch.random.manual_seed(0)

smoothing = 0.1
confidence = 1.0 - smoothing

padding_idx = 0
batch_size = 2
seq_len = 4
size = dim = 10

# model output
x = torch.rand((batch_size, seq_len, dim))
x = torch.log_softmax(x, dim=1)
'''
>>> x.shape
torch.Size([2, 4, 10])
'''
x = x.view(-1, size)    # (8,)
# hard target
hard_target = torch.randint(1, size-1, (batch_size, seq_len))        # 0~9
hard_target[0][seq_len - 1:] = padding_idx
'''
>>> hard_target
tensor([[3, 8, 1, 0],
        [2, 8, 2, 2]])
'''
hard_target = hard_target.view(-1)  # shape: (8)
# normal distrubytion
norm_dist = x.clone()
norm_dist.fill_(smoothing / size)
'''
>>> norm_dist
tensor([[0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100],
        [0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100],
        [0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100],
        ...
'''
# soft distribution
soft_dist = norm_dist.scatter_(1, hard_target.unsqueeze(1), confidence)
'''
>>> soft_dist
tensor([[0.0100, 0.0100, 0.0100, 0.9000, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100],
        [0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.9000, 0.0100],
        [0.0100, 0.9000, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100, 0.0100],
        ...
'''
# KL Divergence Between Distributions
criterion = nn.KLDivLoss(reduction="none")
kl = criterion(x, soft_dist)
# padding operation
ignore = hard_target == padding_idx
lsm_loss = kl.masked_fill(ignore.unsqueeze(1), 0).sum() / batch_size
"""
>>> lsm_loss
tensor(6.6152)
"""

[참고]

  1. https://blog.si-analytics.ai/21
  2. https://hongl.tistory.com/230
  3. https://github.com/hollance/reliability-diagrams
  4. https://3months.tistory.com/491



© 2021.06. by ekspertos

Powered by theorydb