정보이론[1]
in University / Jekyll on Communications, Blog, Github, Pages, Jekyll, Spacy
개요
통신, 신호처리, IOT, 정보보안, 머신러닝 등 다양한 분야와 밀접하게 관련 있는
정보이론을 알아본다 머신러닝에서 주요하게 사용되는 Cross-Entropy 또한 정보이론에 바탕을 두고 있다
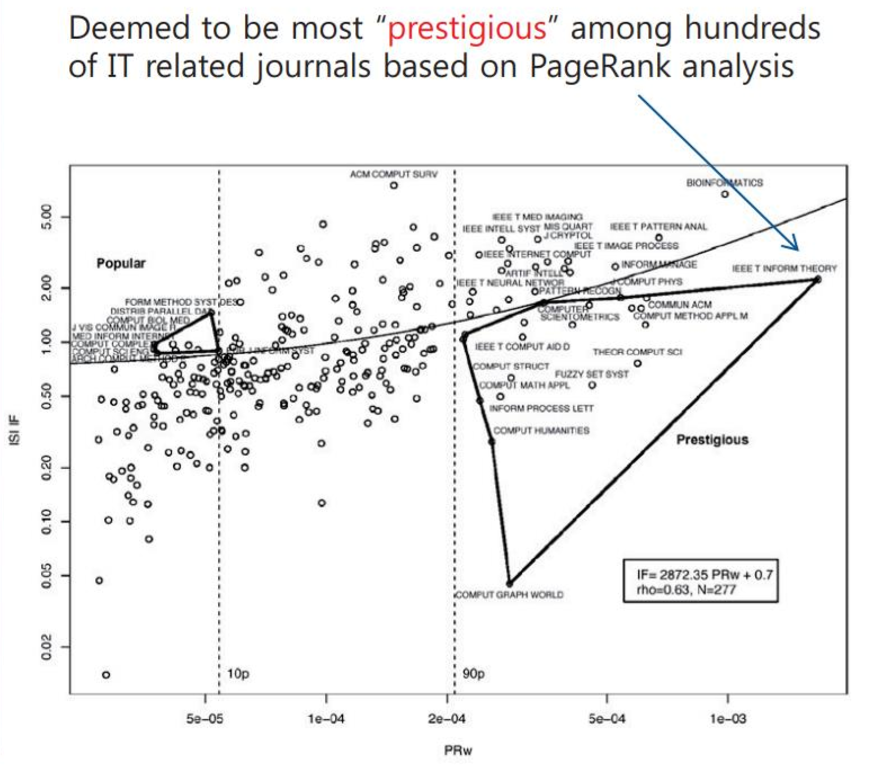
정보이론 관련 이론들은 IEEE Trasaction on Information Theory 에서 발행된다. 다른 저널들의 근윈이 되는 정도를 Prestigious 하다고 하며, 정보이론은 IT 분야에서 가장 높은 Prestigious 수치를 보인다. IT 분야들 중 통신, 신호처리, IOT, 정보보안, 머신러닝과 특히 밀접하게 관련되어 있다.
세로 축은 impact factor, 가로 축은 prestigious 수치를 나타낸다. 가장 오른쪽 위에 위치하는 Information Theory 논문지를 볼 수 있다
밀접하게 관련된 저널들
- IEEE Transactions on Wireless Communications 통신
- IEEE Transaction on Communications 통신
- IEEE Transactions on Signal Processing 신호처리
- IEEE Internet of Things Journal IOT
- IEEE Transactions on information Forensics and Security 정보보안
- IEEE Transactions on Pattern Analysis and machine Intellegence 머신러닝
- IEEE Transactions on Neural Networks and Learning Systems 머신러닝
0. 정보란 무엇인가?
정보이론에서 말하는 정보의 양은 무엇일까? 한 마디로 하면 “불확실성”을 뜻한다
- 오늘 날씨가 좋을 것이다
- 어제 날씨가 안 좋았다
- 내일 날씨가 좋을 것이며 미세먼지 또한 좋을 것이다
이 세 가지 정보들이 가지고 정보량을 따져보면 3 > 1 > 2 순서일 것이다. 2번의 경우 어제의 날씨에 대한 정보가 “안 좋다”는 한 가지 정보만을 갖는다면, 1번은 날씨가 좋을 수도 있지만 안 좋을 수도 있다는 말이므로 정보가 다양해질 가능성이 있다. 3번은 미세먼지에 대한 정보량도 추가되어 정보가 다양해 줄 수 있는 가능성이 더욱 커진다.
“정보가 다양해질 수 있다”는 경우의 수가 크다는 말과 같다. 불확실성이 클수록 나올 수 있는 경우의 수가 많고, 담고 있는 정보량이 많아진다.
1. 정보의 표현
그렇다면 정보를 수치적으로 어떻게 표현할까?
Hartley’s Information Measure
정보는 다음과 같은 특징을 갖는다
- 정보량은 경우의 수와 관련이 있어야 한다
- 정보량은 가산적(Additive)이어야 한다
주사위를 세번 던진 사건은 한번 던진 사건에 비해 3배 더 큰 정보량을 가져야 한다 \[log_b r\]
r은 정보의 경우의 수를 가리킨다. 정보의 가산성을 위해 로그(log)를 사용한다
Hartley’s Information Measure의 오류
정보량의 최소 단위 경우의 수가 2인 사건이 Hartley’s Information Measure에서 가장 작은 값을 갖는다. 이 경우의 정보량은 1-bit 로, Hartley’s Information Measure는 0과 1사이의 정보량을 사용하지 못한다.
경우의 수의 모호함 흰공과 검은 공이 있는 상자에서 공 하나를 뽑는 사건에 대한 정보량은 어떻게 될까? Hartley’s Information Measure은 어떠한 경우에서든 1-bit 로 사건이 표현된다. 흰공이 1개 검은 공이 1개인 경우여도, 흰공이 1000개 검은 공이 1개인 경우여도, 모두 1-bit로 표현된다. 그러나 생각해보면 흰공이 1000개이고 검은공이 1개인 경우 상자에서 뽑는 공이 흰공일 것이라고 쉽게 예측 가능하다. 다음과 같은 사건들은 보통 사건 보다 적은 정보량으로 표현되면 좋을 것 같다.
Shannon’s Information Measure
Shannon은 사건이 일어날 확률을 포함하여 점보량을 정의한다 \[H(U) = - \sum_{u \in supp(P_U)} P_U(u) log P_U(u)\]
모든 경우들에 대해 갖는 확률이 같다면, Shannon과 Hartley의 Information Measure이 같아진다
2. 이산확률 (Discrete Probability Theory)
이산확률은 다음 3 가지 요소를 바탕으로 한다
- Sample Space $ \Omega $
- Events
F - Probability Measure
Pr( )
Sample Space
랜덤 출력으로 나올 수 있는 모든 출력들이 집합이다 \(\Omega = \{ w_1,w_2 ... w_n \}\)
Events
Sample Space의 부분 집합이다 \(F = \{ \varnothing, \{ w_1 \}, \{ w_2 \}, \{ w_1, w_2 \} ... \} \\\) $w_1$ 또는 $w_2$ 가 나타나는 사건을 ${ w_1, w_2 }$ 로 표현한다
Probability Measure
Sample Space의 확률을 다음과 같이 표현한다 \(Pr(\Omega) = 1 \\ Pr(\varnothing) = 0 \\ ...\) Atomic Event : 단일 Sample Point 만 포함하는 이벤트 Cardinality : 집합의 크기 (위의 예에서 n)
랜덤 변수로 사용되기 위해 알파벳으로 매핑해 주어야 하며 보통 실수를 사용한다. \(w_1 -> 1, \ w_2 ->2, \ w_3 -> 3 ...\)
Estimation & Average
\(E[g(x)] = \sum P(x)g(x)\) 분산은 다음과 같이 표현된다. (제평평제) \(\sigma^2 = E[X^2] - (E[X])^2\)
LLN (Law of Large Numbers)
Sample Space에서 무작위로 뽑은 Sample들의 평균이 전체 모집단의 평균과 가까울 가능성이 표본의 수가 증가할 수록 높아진다. Weak LLN \(P(|\lim_{n->\infin}\bar{X} - \mu| < \epsilon) = 1\) Strong LLN 채널코딩 이론을 증명하는 과정에 사용된다. \(P(\lim_{n->\infin}\bar{X} = \mu) = 1\)
Central Limits Theorm
모집단의 분포와 상관없이 표본의 크기가 커지면 표본 평균의 분포가 정규분포에 가까워진다. 모집단에서 무작위로 여러개 추출한 것을 표본이라고 하며 그 이에 대한 평균을 표본평균이라 한다.
example)
모집단 : {0, 1}
표본 크기 : 4
표본 : {0,0,0,0}, {1,0,0,0}, {1,1,0,0} ...
표본의 평균 : 0, 0.25, 1, 1.25, ...
표본을 만들 때마다 표본 평균 값을 얻을 수 있고, 만들어지는 평균들으로 분포를 만들어보면 이 분포는 정규분포에 가까운 것을 확인 할 수 있다 표본의 크기가 커지면 커질 수록 정규분포에 가까워진다.