전자회로2

Widlar current source

작은 전류에서 사용한다 더 작은 저항 값을 사용할 수 있다

Wilson current source

출력 임피던스 크게 하려고 사용한다

Differential Amplifier

Differential Amplifier을 사용하는 이유

noise에 덜 민감하다 큰 CMRR을 갖는 증폭기를 설계할 수 있다
Direct Coupling이 가능하다 출력에 DC가 포함되지 않아 Direct coupling이 가능하다
Source 단에 bypass capacitor이 필요없다 Rss 가 differential gain에 영향을 주지 않는다
Gate Biasing이 필요없다
DC Amplifier로서 사용이 가능하다

BJT와 MOSFET Large Signal Analysis

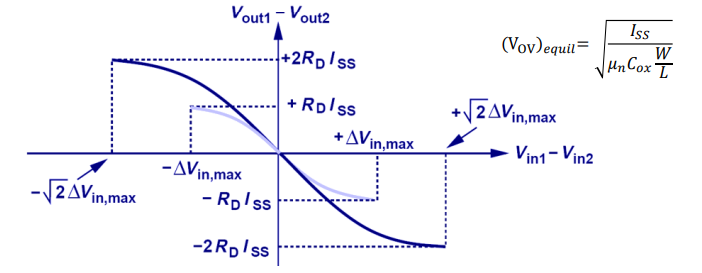
BJT와 MOSFET 차동쌍 회로의 대신호 특성 곡선을 비교한다

BJT : 0.06V 차이에서 $0.91I_{EE}$ 만큼의 전류가 쏠린다(absolute bound)
MOSFET : 0.06V 차이에서 $0.65I_{EE}$ 만큼의 전류가 쏠린다

BJT의 경우 slope이 가파르기 때문에 더 큰 증폭값을 사용할 수 있다.

지수승을 사용하는 BJT의 경우 더 빠르게 $I_{EE}$ 값이 한쪽으로 기울어진다

대신 MOSFET은 모든 전류가 한쪽으로 쏠리는 지점이 있지만 BJT의 모두 쏠리는 지점을 찾을 수 없다.

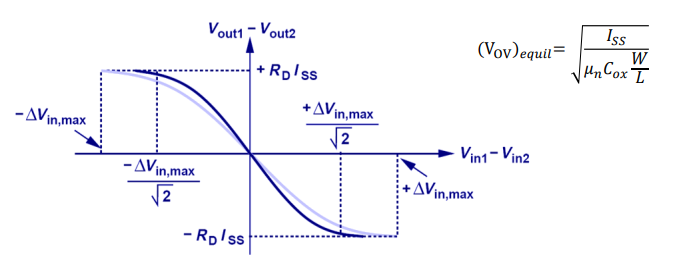
MOSFET Linearity trade-off

$V_{ov}$ , Over-drive Voltage를 증가해줌으로써 전류와 전압 간의 linearity를 증가시킬 수 있다. 그러나 그 trade-off로 더 많은 파워가 필요하며, 기울기 즉, gain이 줄어든다.

Tail Current x2 differential output swing 또한 그에 비례하여 증가한다
W/L x2 입력으로 가질 수 있는 전압 범위가 좁아질 뿐 output swing이 달라지지 않는다

Common Mode Amplifier

Common Mode로 동잘하는 경우 왜 증폭이 0일까? Common mode로 사용하는 경우 증폭값이 다음과 같다 $A_v = -\frac{\triangle R_D}{\frac{1}{g_m} + 2R_{EE}}$

이때 ideal current source를 사용하면 증폭값은 0 이 된다

그러나 ideal하지 않은 현실에서는 증폭이 조금은 생긴다

반면에 Differential mode로 동작하는 경우, 중앙을 virual ground로 볼 수 있어 다른 식을 사용해 증폭값을 정의하게 된다 \[A_v = -g_mR_D\]

Active Load

DISO 를 위해서 diode-connected load 또는 current source load와 같은 Static Load를 사용하지 않는다

current mirror의 Active Load를 사용해 회로를 구성한다 \[A_v = g_mR_D\]

in-phase 출력 신호를 구할 수 있다

Miller Effect

floating capacitor을 두 개의 ground 된 커패시터로 구하는 식이다. 주파수 특성을 파악하기 쉬워진다 \[C_1 = (1-A)C_F \\ C_2 = (1-\frac{1}{A})C_F\]

Miller Effect에 대한 분석은 다음과 같다

feedback 되어 있는 임피던스를 2개의 ground된 임피던스로 바꾸어준다
C2 값은 CF와 비슷한 값을 갖는 반면 C1의 경우 증폭값 만큼의 큰 값을 갖는다 따라서 C1이 커질 수록 wp가 감소하여 midband가 줄어든다 즉 주파수 특성이 나빠진다

internal capacitance external에 비해 작은 값이므로 low pass에 영향을 준다 internal 를 증가 시킨다면, w가 감소하여 low pass 되는 지점이 더 빨리 찾아온다 midband가 줄어들며 주파수 특성이 안 좋아진다.

gain을 줄이거나 feedback이 없도록 만들어 주어야한다 그러나 Intrinsic capacitor 때문에 현실에서는 피할 수 없다

High Frequency Model

Intrinsic Capacitance

BJT

$c_\mu$ base와 collector 사이에 생기는 junction capacitance 이다
$c_\pi$ base와 emitter 사이에 생기는 juction capacitance와 diffusion capacitance를 합한 값이다.
$c_{cs}$ substrate와 collector 사이의 junction capacitance이다

MOSFET

$C_{GD}$ gate와 substrate 사이의 Cox에 gate와 drain 사이의 overlap capacitance를 더한 값이다
$C_{GS}$ gate와 substrate 사이의 Cox에 gate와 source 사이의 overlap capacitance를 더한 값이다
$C_{DB}$ Drain과 Body 사이의 junction capacitance이다
$C_{SB}$ Source과 Body 사이의 junction capacitance이다

Trainsit Frequency

current gain이 1이 되는 주파수 값이다