Linear Block Coding

Systemetic Form

Generator Matrix : \(G = [P | I_{n\times n}]\)

Parity Check Matrix : \(H = [I_{n-k\times n-k} | P^T]\)

Syndrome Testing

신드롬 값을 확인해 에러 발생 여부를 알 수 있다. 에러없이 수신된 경우 : \(S = M \times[P | I_{n\times n}] \times [I_{n-k\times n-k} | P^T]^T = UH^T \\ = P + P = 0\)

에러가 수신된 경우 : \(S = (U+e) H^T = UH^T + eH^T = eH^T\)

에러가 없을 경우에는 신드롬 테스트의 결과가 0이지만 에러가 수신된 경우 0이 아니게 된다

신드롬은 [1xn-k], $ 2^{n-k} - 1 $ 개의 에러 패턴을 correction 할 수 있다. -1을 해준 이유는 모두 codeword가 all zero 일 경우 error free 이기 때문이다

모든 1-bit 에러에 하나의 2-bit 에러를 더 correction 할 수 있다.

minimum distance 확인하는 방법 : parity check matrix H의 상태를 확인한다

• H에서 모두 0인 열이 있는 경우 : d = 1 (6,3)에서 3번째 열이 모두 0이라고 한다면, 001000을 수신하면 syndrome testing 결과가 0이 나온다 이는 minimum hamming weight가 1이라는 뜻이다.

• H에서 같은 값의 열이 있는 경우 : d = 2 (6,3)에서 3번째 열과 4번째 열이 같다면, 001100을 수신하면 syndrome testing 결과가 0이 나온다 이는 001100이 codeword라는 의미이며, minimum hamming weight가 2이다.

• H에서 모든 열이 linearly dependent한 경우 : d = n-k

사용되는 분야

• 통신 error check
• SSD error check
• 위성 통신 error check

reed-solomon : (255, 239) 모든 8byte correction

LDPC (Low Density Parity Check Code) Generator matrix : 64000 x 64000 행렬 64000개 중 극소수만 0이 아닌 1 이다 현재 5G에 사용된다 SSD channel coding에 쓰인다

Cyclic Block Coding

Cyclic Code란

cyclic 코드들은 다음과 같은 특성을 갖는다

1. codeword를 shift한 것 또한 codeword 이다
2. LFSR을 이용해서 쉽게 구현 가능하다

n개의 요소로 이루어진 codeword는 다음과 같이 표현 할 수 있다 \(U(x) = u_0 + u_1X + u_2X^2 + ... + u_{n-1}X^{n-1}\) n-1 승 혹은 그 이하로 모두 표현할 수 있다

해당 codeword을 이용해 cyclic codeword들을 모두 구하기 위해 다음을 사용하면 된다. \[X^n + 1\]

codeword를 shift한 후 $ X^n + 1 $로 modular 연산을 하면 cyclic 된 codeword를 얻을 수 있다.

위의 예는 codeword를 통해 cyclic codeword를 만드는 예이다.

Gereator Polynomial

앞서 우리가 알아본 것은 cyclic codeword를 이용해 cyclic codeword를 알아내는 과정이다. 이번에는 Linear block code에서와 같이 generator polynomial을 이용해서 message에 대한 cyclic codeword를 만들어 줄 것이다.

generator polynomial g(x)는 Cyclic code의 특성을 유지하기 위해 $ X^n + 1$ 과 동일한 특성을 가지고 있어야한다. 그러면서 message polynomial을 codeword polynomial로 바꿔줘야한다.

따라서 다음 두가지를 만족한다

1. codeword가 n-1 degree이고 message가 k-1 degree이면 generator polynomial은 n-k degree 이어야 한다 (7,3) 코드의 예 \(C = X^{6} + ... \\ M = X^{3} + ... \\ G = X^{3} + ... + 1\)
2. Cyclic 특성을 갖기 위해 $X^n + 1$가 인수분해된 값들을 이용해야 한다 \(X^7 + 1 = (1 + X + X^3)(1 + X + X^2 + X^4)\) 이므로 인수분해된 두 개를 generator polynomial로 사용할 수 있다.

LFSR을 이용해 다음과 같이 구할 수 있다.

m(x) 에 (n-k)-bit shift 해준 뒤 mod g(x) 해준 결과가 p(x) 이다. \[X^{n-k}m(x) = q(x)g(x) + p(x)\]

p(x)를 양 변에 더하면 다음과 같다 \(X^{n-k}m(x) + p(x) = q(x)g(x)\)

이는 generator polinomial g(x)에 q(x)를 곱한 것과 같은 형태이다.

 LFSR으로 구해진 나머지 값을 이용해 전송을 하면 p(x)g(x)의 형태를 갖는다는 것이 중요하다
 수신단에서 동일한 LFSR을 이용한 모듈러 연산을 하면, syndrome test를 할 수 있다.
 LFSR을 모두 통과한 후 에러가 없다면 shift register 값이 0이고 에러가 있다면 LFSR에 남아있는 값이 0이 아닐 것이다

이것이 중요한 것이 decoding 단계에서 g(x)를 이용해 나누어주면 된다는 것을 알 수 있기 때문이다.

encoding 단계에서 n-k time 동안 m(x)값을

1. n-k 만큼 m(x)를 shift 한 후 g(x)를 이용해 modular 값을 구한다
2. 구해진 값을 m(x) 뒤에 redundancy로 붙여준다
3. [p(x)|m(x)] 상태는 g(x)q(x) 와 같은 형태라고 볼 수 있다
4. 그러므로 수신부에서 U(x)를 g(x)로 modular 하면 0의 결과를 얻을 수 있다

즉, decoding 단계에서 g(x)를 나타내는 LFSR을 지나면 shift register에 저장된 결과가 모두 0 이어야 한다

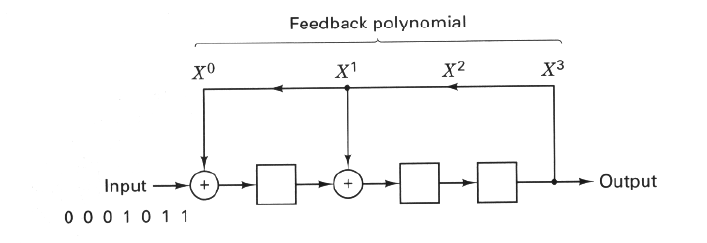
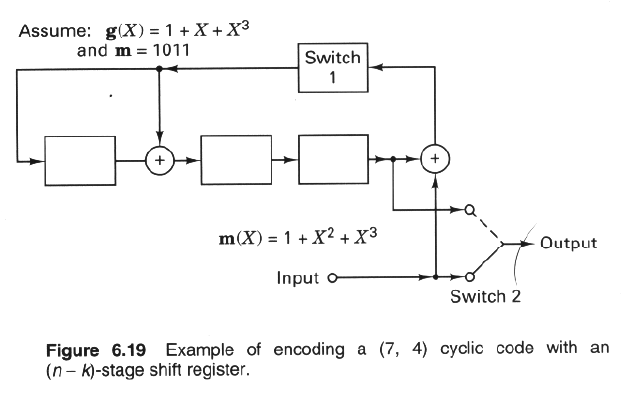
구현은 LFSR을 이용해 다음과 같이 할 수 있습니다. 다음과 같은 형태는 n-bit 입력을 통해 동작한다. 메시지에 (n-k) zero bit 들을 추가해 입력으로 사용한다 shift가 완료된 후의 값이 나머지 값 p(x) 이며 메시지에 추가해 전송한다

이와 같은 형태는 k-bit 만을 입력으로 사용한다. input k-bit 동안은 switch 2를 동작 시키고 다음 n-k 동안은 동작시키지 않는다. k-bit 동안은 message를 받고 나머지 n-k bit 동안은 나머지 값들을 얻는다

Perfect Code

최근방 복호법으로 복호할 때, 복호 실패 없이 반드시 복호 가능한 부호이다. 통상 오류정정능력 보다 많은 비트 오류가 발생하면 복호 오류가 언제든 발생하므로 완전 뷰호는 매우 드문편이다.

$2^n$ 개의 codeword를 모두 매칭 시켜줄 수 있다.