Shannon Capacity

정보이론의 아버지 클로드 섀넌에 의해 발전된 이론이다.

채널 용량(Channel Capacity)는 정보가 에러를 발생시키지 않고 보내질 수 있는 최대의 속도를 말한다.

spectral efficiency : \(C = log_2(1+SNR) \ \ bps/Hz\) Data Rate : \(C = W log_2(1+SNR) \ \ bps\)

Average spectral efficiency가 1인 시스템은 정말 좋은 시스템으로 현존하는 시스템 중에서도 두 개 정도만이 이 조건에 근접해 있다.

• 4G : spectral efficiency between 0.074 to 6.1 bits/s/Hz
• 5G : 5G networks promise efficiencies of between 0.12 - 30 bits/s/Hz

Data Rate를 증가시키는 방법 \(C = W log_2(1+\frac{\alpha P_{TX}}{N_0 W}) \ \ bps\) attenuation coefficient는 수신까지 발생하는 감쇄의 정도로 제어가 불가능하다. 일반적으로 자유공간에서 거리에 제곱만큼 감쇄가 일어나며 도심에서는 세제곱만큼 일어난다.

• Transmission power는 W로 표현하지 않는 이유? Noise Power는 bandwidth 증가에 따라서 같이 증가하지만, 송신 파워는 규격이 정해져 있기 때문에 bandwidth를 증가시키면 그에 따른 Power Spectral Density(PSD)를 감소시켜야 한다.

1. 송신 출력 증가

   [전파법]
   '국내 공유기 출력은 20dbm이하로 제한된다'
   

   전파법에 위반되지 않는 선에서 송신출력을 높여줄 수 있다.

2. 대역폭 증가 사용하는 bandwidth를 증가시킨다. 수십 GHz 이상 사용하면 log 안에 있는 1/W에 의해 saturation이 발생한다. 그러나 아직까지는 GHz까지 사용하는 시스템이 없다. 5G 의 경우에는 single channel에서 4G의 4배에 해당하는 대역폭을 사용해 data rate을 늘린다.

Eb/N0 (Energy Per Bit to Noise Spectral Density Ratio)

아날로그 통신에서는 전력이 유용한 척도가 될 수 있으나, 디지털 통신에서는 전력 보다는 에너지가 보다 유용한 척도가 된다.

\(\frac{E_b}{N_0} = \frac{S \times T_b}{N/W} = \frac{S}{N}\times \frac{W}{R}\) Bit time Tb, bandwidth W, data rate R 을 사용해 표현한다. 분자로 에너지 신호, 분모로 PSD 신호를 갖는다.

디지털에서는 하나의 메시지가 1bit, 2bit, 3bit, … 등을 이용할 수 있다. 이 경우에 한 time에서의 평균적인 파워를 보게되면 다 똑같이 보일 것 이다. 이 메시지가 가지고 있는 bit들을 구분하고 그 bit들이 개별로 갖는 SNR을 보여주기 위해 Eb/N0을 사용한다.

예를들어 현재 SNR이 20이라고 하자. 메시지가 1bit를 의미할 경우 1bit의 S/N이 20이고 메시지가 10bit를 의미할 경우에는 1bit의 S/N이 2로 줄어든다.

1bit Eb/No + 1bit Eb/No + 1bit Eb/No … = SNR

노이즈 신호는 correlation이 없는 신호고 메시지 신호는 correlation이 있기 때문에 이런 식으로 계산된다 \[\frac{(b+b+b)^2}{a^2 + a^2 + a^2}\]

Eb는 1bit information 당 수신된 에너지이다.

Channel Coding의 장점

Redundancy Bit들를 추가해 데이터를 전송한다 redundancy를 추가해 information의 datarate가 감소한다는 단점이 있지만 그에 비해서 장점이 더 크다.

coding rate : \(C = k/n\) channel coding 전 datarate k(physical throughput)와 channel coding 후의 datarate n(mac throughput)을 이용해 coding rate를 구해준다.

Eb/N0 : \(\frac{E_b}{N_0} = \frac{1}{C} SNR\) 위 식을 이용해 channel coding의 장점을 알 수 있다.

채널 코딩을 하면 우리가 송신한 information 데이터에 대한 Eb/N0이 좋아진다. C = 1/2 인 경우 즉 1bit information을 2bit로 송신한 경우를 살펴보자.
수신단에서 1 bit 당 10dB 만큼의 SNR 값을 갖는다면 information은 2bit에 대한 정보이므로 총 10dB + 3dB 만큼의 SNR 값을 갖는다 \(\frac{E_b}{N_0} = \frac{1}{C} SNR = 2 \times SNR = 10dB + 3dB = 13dB\)

SNR이 동일한 상황에 channel coding을 하면 더 좋은 SNR로 신호를 수신할 수 있다.

bit에대한 에너지도 증가하지만 노이즈 파워도 증가된다. 그러나 Eb/N0이 2배가 된 이유는 다음과 같다. \(\frac{(b+b+b)^2}{a^2 + a^2 + a^2}\)

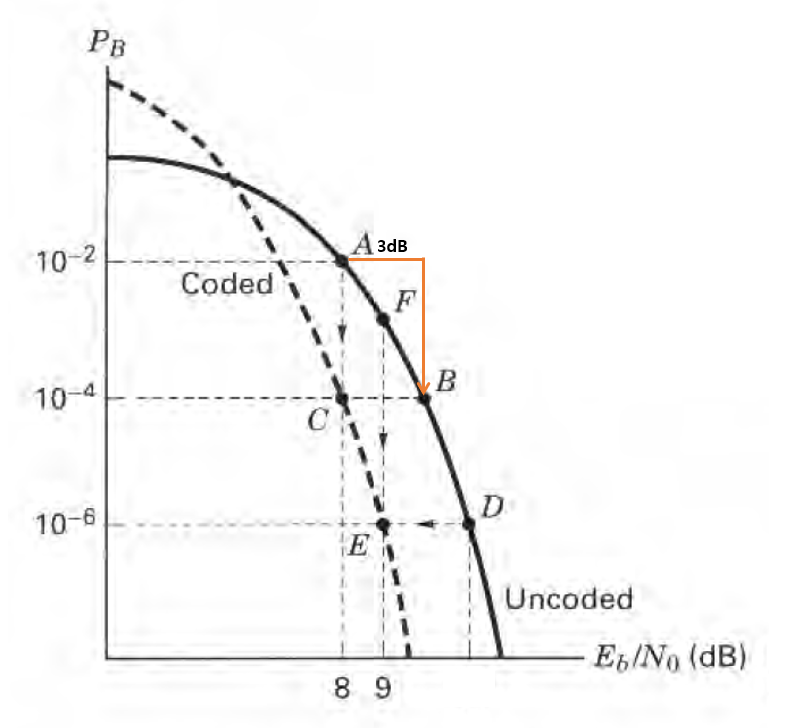
예시로 다음과 같은 그림이 있다

우리의 기존 Eb/N0이 8dB라고 하면 1/2의 coding을 추가하면 SNR이 2배 즉, 3dB가 늘어난 상태로 information bit들이 수신된다. 원래 10e-3이였던 BER가 10e-5이 된 것을 볼 수 있다.

다른 기준으로 보면 8dB에서 동작했던 시스템을 5dB에서도 동작 시킬 수 있다 좀더 열악한 통신 환경에서도 동작할 수 있다는 뜻이다

Error Performance VS bandwidth

information에 대한 datarate을 동일하게 유지하면서 performance를 좋아지게 하고 싶으면 채널 코딩을 하면 된다. 그러나 채널 코딩을 추가하려면 더 큰 대역폭을 사용해야 한다

Power VS bandwidth

송신 출력을 줄이고 싶다. 같은 Eb/N0을 갖지만 채널 코딩을 사용하면 SNR이 1/2배가 된다. 필요한 SNR이 줄기 때문에 송신출력을 줄여줄 수 있다. 그러나 채널 코딩을 추가해야 하므로 더 큰 대역폭을 사용해야 한다

Data Rate VS Bandwidth

동일한 대역폭을 사용하면서 datarate을 증가시키면 Eb/N0이 줄어들 것 이다. 동일하게 중가시켜준 대역폭이 필요하다

`