서론

그래프 문제를 트리 문제로 모델링하는 알고리즘 Heavy-Light Decomposition을 소개한다.

알고리즘 문제들을 풀다보면 많은 경우 문제들을 그래프로 모델링 할 수 있다. 여러 요소들 간의 관계가 주어지는 경우 각 요소를 정점으로 관계를 간선으로 하는 모델화가 자주 사용되고 DP 문제는 DAG(Directed Acyclic Graph)로 각 상태가 이어지는 것을 보게된다.

일반적인 형태의 그래프라면 효율적인 계산이 매우 어렵거나 다항시간 안에 해결하는 것이 불가능한 문제들도 보게된다. 그래프 문제를 트리 형태로 모델링 한다면 보다 적은 시간 복잡도로 문제를 해결할 수 있게된다. 예로 최단 경로 탐색 문제에 HLD를 사용하면 $ O(log^2N) $의 시간복잡도로 문제를 해결한다.

이번 글에서는 트리이기 때문에 사용할 수 있는 테크닉 중 하나인 Heavy-Light Decomposition에 대해 기본적인 설명과 이를 사용해 어떤 문제들을 풀 수 있는지 알아보겠다.

관련 문제

1. 백준 13510 - 트리와 쿼리 1 (https://www.acmicpc.net/problem/13510)

Heavy-Light Decomposition

일반적인 트리에서 경로를 나이브하게 구하고자 한다면 트리를 순회하기 때문에 정점의 개수가 N개인 트리에서 O(N) 시간이 소요되기 때문에 효율적인 방법이 필요해진다. HLD 테크닉은 트리를 1차원 백터들로 분할하여 마치 1차원 백터의 묶음 처럼 다룰 수 있다. 여러 1차원 백터를 다루는 것이 트리를 다루는 것에 비해 더 적은 시간복잡도가 요구된다.

수행방법

채인과 채인 사이의 이동이 적을수록 더 적은 시간 안에 알고리즘을 수행하게된다. 채인의 수는 적도록 채인 하나하나의 길이는 길도록 채인들을 분할한다.

아래 그림은 채인으로 분할되는 과정을 보인다. 각 정점에 쓰인 수는 해당 노드를 루트로 하는 서브트리의 노드 수를 의미한다.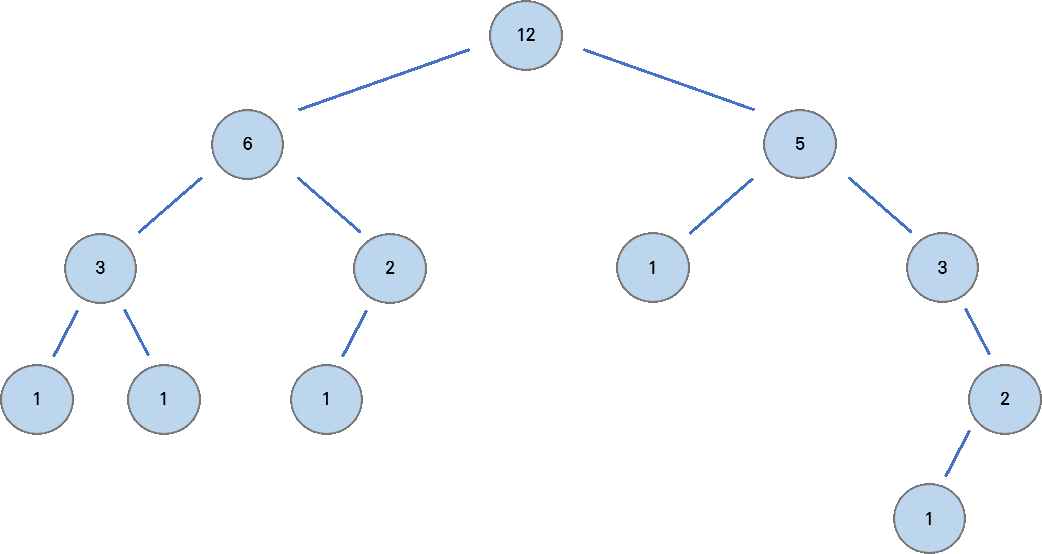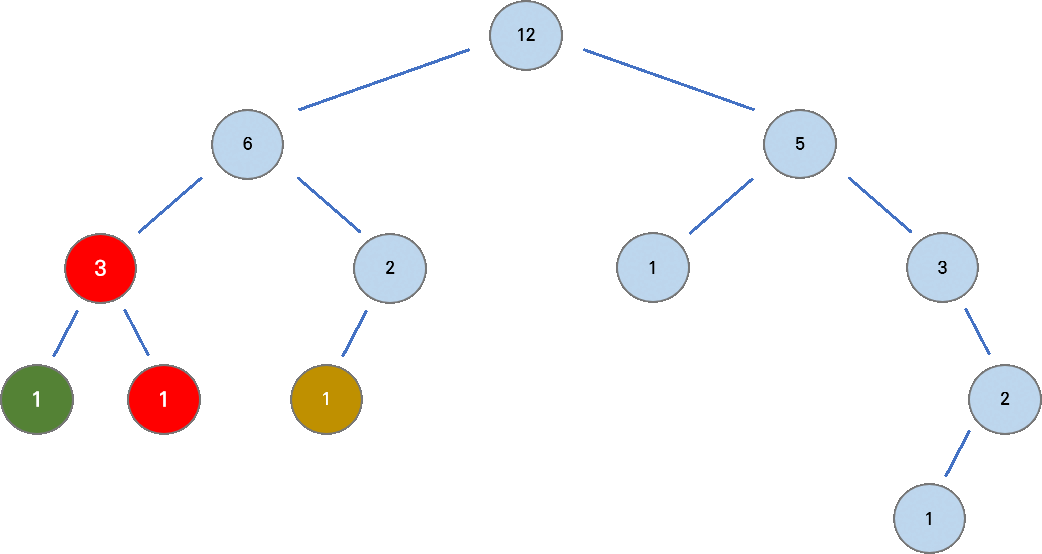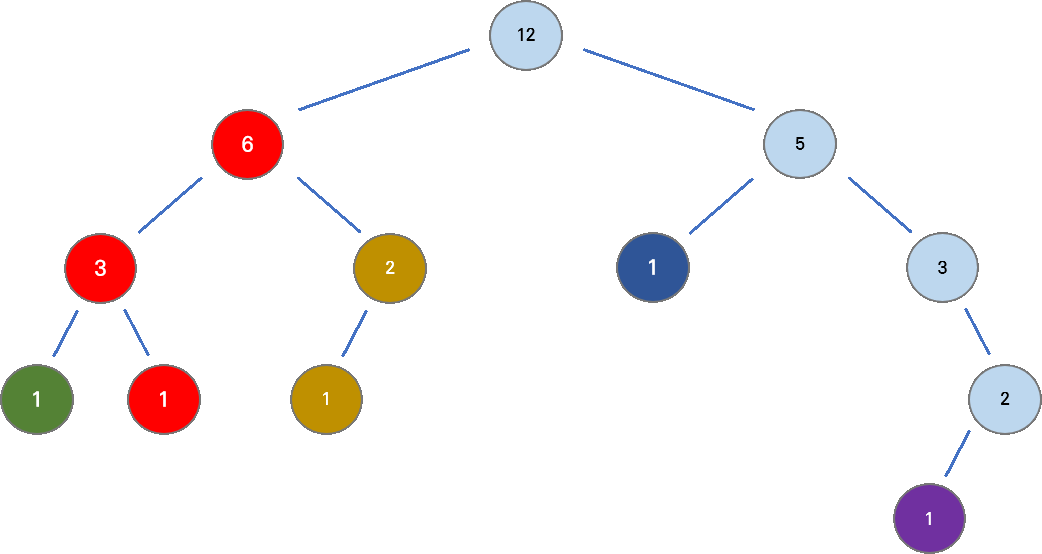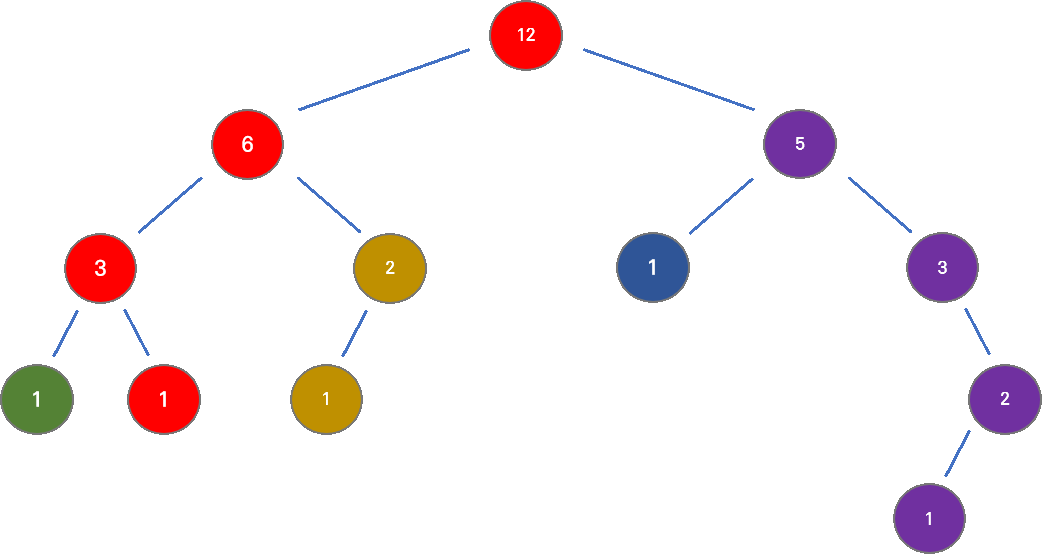

서브 트리의 노드 수가 가장 많은 자식 노드와 채인이 연결된다. 나머지 자식 노드들은 자신을 루트로 또다른 채인을 구성하게 된다.

1. heavy 노드를 찾는 과정 서브 트리의 노드 수가 가장 많은 자식 노드, Heavy node를 찾는 과정이다. depth first search를 사용한다.

int dfs(int cur) {
	/*
	information:
		Depth First Search 이용한 Tree 구성
	input:
		cur - 현재 node 정보
	update:
		parent - 부모 node 정보
		weight - parent node와의 간선 weight 정보
		depth  - Tree에서 depth 정보
		heavy  - 무게가 무거운 child 노드 정보
	return:
		size - 노드의 무게 (아래 노드들의 합)    */

	int size = 1, maxsize = 0;
	for (auto& i : adj[cur]) {
		int next = i.first;
		if (parent[cur] == next) continue;
		parent[next] = cur;
		weight[next] = i.second;
		depth[next] = depth[cur] + 1;

		int tmp = dfs(next);
		if (tmp > maxsize) {
			maxsize = tmp; heavy[cur] = next;
		}
		size += tmp;
	}
	return size;
}

1. Decompose 과정 1번에서 구한 결과를 사용해 chain들로 분할한다

   void decompose(int cur, int h) {
     // chain으로 분할
    head[cur] = h;
    seg[seg_idx] = weight[cur];
    pos[cur] = seg_idx++;
    if (heavy[cur] != 0) {
        int next = heavy[cur];
        decompose(next, h);
    }
    for (auto &i : adj[cur]) {
        int next = i.first;
        if (parent[cur] != next && heavy[cur] != next)
            decompose(next, next);
    }
   }
   

   ---

참고

djm03178님 블로그 https://www.secmem.org/blog/2019/12/12/HLD/