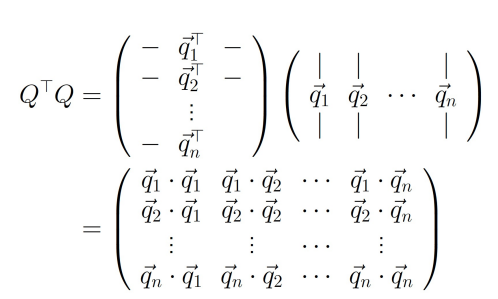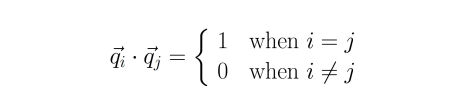QR factorization

QR 분해 사용 이유

condition number를 따라 구해진 해의 정확도를 올릴 수 있다. Ax = b에서 x의 정확도를 A의 condition number을 통해 알 수 있다.

$ cond(A) =

A^{-1}

\

A

$

choleskey factorization 의 condition number는 $cond(A^TA) = (cond(A))^2 $ 이다. 큰 condition number로는 정확한 x 값을 구할 수 없다 이번 글에서 더 낮은 condition number 을 사용해 해를 구할 수 있는 방법을 알아본다

QR 분해 condition 값

역함수가 존재하는 행렬을 B를 곱하는 것은 행렬의 column space에 영향을 주지 않는다 \(colA = colAB\) Ax = b 는 A의 column space를 이용해 b를 구할 수 있는 방법을 알아내는 문제이다

동일한 column space를 사용하는 행렬로 바꾸어 주는 것은 값을 구하는데 영향을 주지 않는다.

우리는 A를 사용해 다음과 같은 특성을 갖는 행렬을 만들어 줄 것이다

\(AR^{-1} = Q \\ Q^TQ = I \\ cond(I) = 1\) QTQ가 Identity Matrix가 되도록 행렬을 찾아줄 것이며 이를 이용하면 더 낮은 condition number로 해를 구할 수 있다 \[Ax = b \\ AR^{-1} R x = b \\ QRx = b \\\]

Rx = y 를 조건으로 하여 Qy = b, Rx = y 두 식을 풀어 x를 구한다

1. Qy = b \(Q y = b \\ Q^TQy = Q^Tb \\ Iy = Q^Tb \\\) least-square 을 이용한 방법이다. Indentity Matrix I의 condition number 는 1 이다 cond(I) = 1

2. Rx = y \(Rx = y \\\) 행렬 R의 condition number을 통해 구할 x 값을 구할 수 있다.

결론적으로, 원래 $cond(A)^2$ 의 행렬을 이용하는 대신 $cond(R)$ 의 행렬을 이용해 구할 수 있다

Q : Othogonal Matrix R : Upper Triangular Matrix

$Q^TQ = I$ 위한 조건

$Q^TQ = I$ 가 되기 위한 조건을 알아본다

다음 조건들을 만족하면 $Q^TQ = I$ 를 만족한다고 할 수 있다

• 행렬 Q의 모든 열이 unit vector 이다, $

  \overrightarrow{v_i}

  = 1$

• 행렬 Q의 모든 열이 정규 직교의 특서을 갖는다

이러한 특성을 만족하는 행렬을 Othogonal Marix 라고 한다

• Isometry Properties Q를 x 에 곱합면 x를 rotate, reflect 하지만 shearing, stretching을 하지 않는다

QR 행렬 구하는 법

A 행렬을 이용해 Q를 구한 후 그 값들을 이용해 R을 구해주는 방법을 알아본다

Gram-Schmidth Ortogonalization 을 이용해 행렬 Q를 구한다 다음 두가지를 통해 구할 수 있다.

1. Rescaling to Unit Length
2. Subtracting off projection

기존의 vector들에 수직하면서 unit-vector을 구하는 것이 목적이다

백터 (v1, v2) 이 Orthonormal 하도록 만들어준다 orthonomal 한 백터들을 (a1, a2) 라고 한다 1. \(a_1 = \frac{v_1}{|v_1|}\) 2. \(v_2' = v_2 - (v_2\cdot a_1)\times a_1 \\ a_2 = \frac{v_2'}{|v_2'|}\) v2 에 있는 a1 방향의 크기를 내적으로 이용해 구한 후 a1을 곱해 a1 방향의 백터로 만든다

백터 v2 와 v2’를 빼주어 a1 방향 성분에 수직인 값을 얻을 수 있다

위 방법을 통해 Q를 구한 후 $R = Q^TA$로 R을 구한다 \[A = QR \\ Q^TA = Q^TQR = R\]