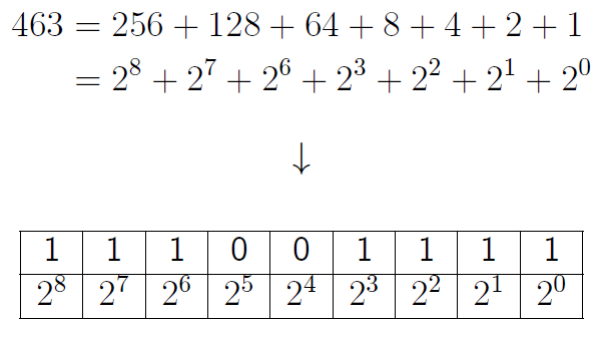
Numerical Algroithms
## 서론
수치를 표현하는 방법에 대해 소개한다
Fixed-Point Representation
변수 k와 l을 사용해 표현한다 \(2^{-k} \sim 2^l 를 \ 이용한 \ 표현\)
- 특징
k + l + 1자리수를 사용한다- $ 2^{k+l+1} $,
k = 2,l = 7라면 1024 가지 수 표현 가능 하다 - 정수 사칙 연산에 유용하다
- 모든 자리수에 $2^k$ 를 곱하여 정수 연산 진행 후 $2^k$를 나누어 준다
- 단점
- 곱하기와 나누기 연산의 경우 표현 가능 범위를 쉽게 벗어날 수 있다
- 스케일이 굉장히 큰 곳에서 사용 불가능하다 $ 9.11 \times 10^{-31} , 6.02 \times 10^{23} $ 두 숫자를 모두 표현해야 될 경우
Compact Representation
\(6.022 \times 10^{23}\)
4개의 정확도 자리수(digits of precision)을 이용해 숫자의 정확도 표현한다고 할 수 있다. \[[6.022 \times 10^{23} - \epsilon, \ 6.022 \times 10^{23} + \epsilon] \ \ , \ \ \epsilon \simeq 0.001 \times 10^{23}\]
\(\alpha \times 10^e\) 로 분리하여 표현하며 이러한 숫자 표현 방식을 부동 소수점 방식이라고 한다.
소수점이 고정된 것이 아닌 변할 수 있기에 부동 소수점이라고 부른다
a: significand (가수)e: exponent (지수)
Floating Point Representation
$0.10\times 2^2 = 1.00 \times 2^1$ 과 같은 경우를 구분해 주기 위해서 보통 $d_0$을 1로 둔다
base: binary 인 경우 2 를 사용precision: 크면 클 수록 값을 더 자세히 표현 가능 (3bit precision -> 1.xx 사용)exp: L와 U 사이의 값을 갖는다

- 특징
- non represented zero 0을 표현하지 못한다
unevenly spaced 표현할 수 있는 첫 숫자가 0.5부터 표현 불가능하다
- Machine Precision 1보다 크면서 가장 가까운 숫자와의 차이로, 위 예에서는 $\epsilon_m = 0.25$ 의 값을 갖는다
Double Precision Floating Point Representation
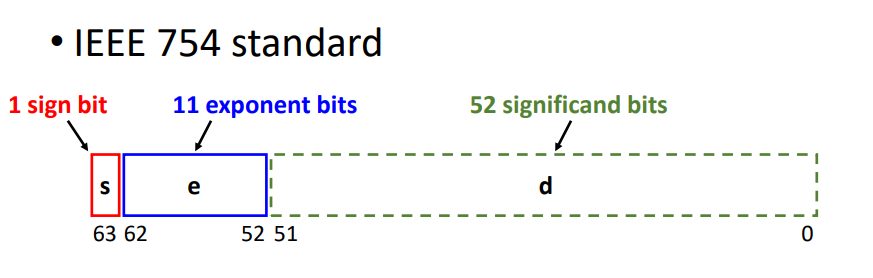
다음은 IEEE 754 표준으로 사용하는 floating point 표현 방식이다. 64-bit 시스템에서 사용된다.
- sign bit : 1 bit
- exponent : 11 bit
all zero: 숫자 0 표현all one: Infinite 표현
- significand : 52 bit
sign bit를 이용해서 precision을 음수 혹은 양수로 표현할 수 있어 double precision이라고 한다.
- 단점 minus 과정이 다소 복잡하다.
Source Of Error
Rounding Error 메모리 한계에 의해 Rounding Error 발생한다
Discretization Error \(v = \frac{dx}{dt} \\ f'(x) = lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
h가 0에 근접하도록 divided difference를 사용하며 이 과정에서 error 발생한다.Modeling Error 처음부터 모델링을 잘못하여 error가 발생한다
Input Error 입력 초기값을 잘못 주어져 input error가 발생한다